Statistical designs for studies seeking to understand COVID-19 transmission in schools

Prepared for the DELVE Initiative by Richard Wilkinson, Nick Latimer, Bill Browne, Simon Burgess, Michael Campbell, David Ellis, Sarah Filippi, Axel Gandy, Inès Hassan, Anna Vignoles

Citation

Richard Wilkinson, Nick Latimer, Bill Browne, Simon Burgess, Michael Campbell, David Ellis, Sarah Filippi, Axel Gandy, Inès Hassan, Anna Vignoles (2020), Statistical designs for studies seeking to understand COVID-19 transmission in schools. DELVE Addendum SCH-TD2. Published 24 July 2020. Available from https://rs-delve.github.io/addenda/2020/07/24/statistical-design-schools-report.html.

---

BibTeX

@Misc{addenda/2020/07/24/statistical-design-schools-report, title = {Statistical designs for studies seeking to understand COVID-19 transmission in schools}, author = {Wilkinson, Richard and Latimer, Nick and Browne, Bill and Burgess, Simon and Campbell, Michael and Ellis, David and Filippi, Sarah and Gandy, Axel and Hassan, Inès and Vignoles, Anna}, year = {2020}, publisher = {The Royal Society}, url = {https://rs-delve.github.io/addenda/2020/07/24/statistical-design-schools-report.html} }

Endnote

%0 Generic %T Statistical designs for studies seeking to understand COVID-19 transmission in schools %A Richard Wilkinson %A Nick Latimer %A Bill Browne %A Simon Burgess %A Michael Campbell %A David Ellis %A Sarah Filippi %A Axel Gandy %A Inès Hassan %A Anna Vignoles %D 2020 %F addenda/2020/07/24/statistical-design-schools-report %I The Royal Society %U https://rs-delve.github.io/addenda/2020/07/24/statistical-design-schools-report.html

RIS

TY - GEN TI - Statistical designs for studies seeking to understand COVID-19 transmission in schools AU - Richard Wilkinson AU - Nick Latimer AU - Bill Browne AU - Simon Burgess AU - Michael Campbell AU - David Ellis AU - Sarah Filippi AU - Axel Gandy AU - Inès Hassan AU - Anna Vignoles DA - 2020/07/24 ID - addenda/2020/07/24/statistical-design-schools-report PB - The Royal Society UR - https://rs-delve.github.io/addenda/2020/07/24/statistical-design-schools-report.html ER -

APA

Wilkinson, R., Latimer, N., Browne, B., Burgess, S., Campbell, M., Ellis, D., Filippi, S., Gandy, A., Hassan, I. & Vignoles, A.. (2020). Statistical designs for studies seeking to understand COVID-19 transmission in schools. Available from https://rs-delve.github.io/addenda/2020/07/24/statistical-design-schools-report.html.

---

• Background
• Research Objectives
• Challenges
• Data Modelling
• Conclusions and recommendations for the design of causal infection testing
• Footnotes and References

Background

A fundamental question in any discussion of the costs and benefits of school closures is to understand the change in risk to children and staff of contracting COVID-19 in school. The risk is a function of the proportion of children infected, transmission within the school environment, and immunity in children.

Scientific knowledge about the role of children in the transmission of the SARS-CoV-2 virus is still developing¹. Children consistently appear to be less susceptible to infection than adults, particularly younger children, with secondary attack rates estimated to be about ⅓ of those seen in adults². The relative infectiousness and viral load of children versus adults is still uncertain. Even once our knowledge of these fundamentals improves, we cannot easily use this information to predict the effect that opening or closing schools will have on risk levels, as this depends upon the environment and facilities of the school, and the behaviour of those attending school. It is important to also consider the risks to children not in school, and it should not be assumed that returning to school is riskier than not doing so. Children not attending school will inevitably begin to socialise: parents struggling with working from home whilst attempting to home-school their children will start to pool their efforts, and there is a risk that non-school transmission in children will increase. Given the costs and harms of keeping children out of school (in terms of both health and learning loss), we need to be sure of the relative transmission rates in children at school versus not in school.

Most schools in England are not fully operational, with, for example, the majority of primary schools only open for reception, year 1, and year 6 children. This creates a brief opportunity to conduct a large-scale study looking at relative infection rates in children attending and not attending school. Infection rates will vary by region, school type, socio-economic background etc., and dealing with these confounding variables in an observational study would be difficult. The current partial opening of schools creates a natural experiment: by measuring children who are both attending and not from the same school, we have the opportunity to get as close as is feasible to a randomised controlled trial which controls for confounding variables. Children that are matched in background and community, have been assigned to the two treatment groups (permitted to attend or not permitted to attend) with relatively little confounding between treatment and risk³. This gives us a short and unique opportunity⁴ to estimate the relative risks of: (1) attending school vs not attending school, and (2) being permitted to attend school, vs not being permitted to attend school. This could provide valuable information on the effect on the infection rate of attending school, and also on the impact of a policy that allows schools to re-open - recognising that even if permitted, some children will not attend school.

PHE’s COVID-19 Surveillance in KIDs (sKIDs) programme⁵, which began in mid-June, aims to test staff and students in 100 schools this mini-half term (testing the same individuals in each of four consecutive weeks), with plans for a wider roll-out for the start of the autumn term. Schools will be asked to participate in one of two arms of the study: (a) sero-surveillance (three samples over 6 months) or (b) weekly nasal swabbing (RT-NAAT tests) until the end of the summer term, with participants invited from children who are currently attending preschool, primary and secondary school as well as staff. sKIDs does not currently plan to test children not attending school.

We discuss the design of the sKIDs programme, what we may hope to learn from this study, and how alternative designs may increase its effectiveness. We focus on estimating prevalence, rather than cumulative incidence, but the analysis and conclusions would be similar.

Research Objectives

sKIDs states that its primary objective is

• to monitor SARS-CoV-2 infection and antibodies in children who are currently attending preschool, primary and secondary school and the school staff

and that its secondary objectives are

• to understand the role of children in the spread of SARS-CoV-2 in preschool and educational settings

• to validate oral fluid and capillary blood testing for SARS-CoV-2 antibodies in children and adults in some participating educational settings

• to evaluate the feasibility of more frequent swabbing in some participating educational settings.

The sKIDs protocol does not explicitly state what effects will be estimated, how they will be estimated (i.e., what data analysis will be done), how much data will be collected, and thus how confident we can expect to be in any conclusions reached given the planned sample size.

To aid discussion of these challenges, we focus on three specific (and narrower) research questions that would feed into the decision making process around school openings:

1. What is the relative prevalence of COVID-19 in children and staff attending and not attending school?

2. What is the effect on the infection rate in children of a policy decision to allow schools to re-open?

3. At what rate does infection spread within schools (both within and between protective bubbles⁶)?

The difference between question 1 and 2 is important. Question 1 describes what is happening at a given point in time. However, to inform policy decisions, it is important to estimate the causal effect on infection rates of allowing schools to open (or to close), given that some parents will choose not to send their children back to school. For a policy maker, this is the more relevant information.

If sufficient data are collected, we might also hope that the data can be used to evaluate the effectiveness of infection prevention and control programmes in schools, and to understand factors associated with any variation in the secondary infection risk, e.g., school type, size, location. However, the low infection rate is likely to mean these questions could not be answered without significantly increasing the number of children tested over that planned by sKIDs, as well as collecting significant volumes of data on what schools are actually doing on the ground which may differ from guidance.

Challenges

Estimating prevalence and transmission rates in schools, and understanding the relative risks of opening/closing schools, is challenging for a number of reasons.

• Infection rates are currently low. The current estimate from the ONS infection survey (18 June) is that an average of 0.06% of people in England had COVID-19 between 31 May and 13 June 2020 (with a 95% confidence interval of 0.02% to 0.13%). A prevalence of 0.06% would mean that fewer than 2% of groups of 30 people (a typical class size) are likely to contain an infected individual (and fewer than 1% of groups of size 15 - the recommended ‘protective bubble’ size for schools). If infection rates are lower in children than in adults, then even fewer cases may be detected. The sample sizes for sKIDs are not yet known, but a large scale survey that tested three classes of size 30 in each of 100 schools (9,000 individual tests) will on average find infection in fewer than 6 different schools. Giving accurate answers to the questions above, and determining whether the risk is increased or not by attending school, is thus likely to be challenging (and based on only a small number of infections).

• The average infection rate for England is uncertain, changing through time, and varies significantly by region: PHE’s Weekly Coronavirus Disease Surveillance Report from 19 June reports up to a 10-fold difference in the weekly-rate of COVID-19 cases between regions. Estimates of the prevalence of COVID-19 in schools are of limited value without paired estimates of the prevalence in children not attending school.

• Schools are currently operating at reduced capacity, with only some year groups able to attend, and subject to forms of infection control that might not be possible under a full opening. Any survey can only assess the risks under the current operating environment. A full opening of schools to all year groups (when more children will be present in the same physical space) may substantially change the risks.

• The act of observing infection via weekly testing (as in sKIDs) potentially changes the infection process. Once an infection in an individual is discovered, their entire bubble will be isolated (i.e., no longer attending school) for at least 7 days, limiting the spread of the virus. sKIDs is thus likely to find only small numbers of infections even in bubbles which contain an infected individual, increasing the difficulty of understanding within-school transmission. In schools not subject to the same level of observation, infections may take longer to be discovered, leading to greater spread and transmission.

Data modelling

Consideration of how the data will be analysed, what data we expect to collect given current estimates of disease prevalence, and thus whether we’ll be able to answer the questions of interest or not, is a useful exercise in evaluation of any data collection protocol.

Expected data

The design of sKIDs is to test individuals grouped within schools and within bubbles. Let $y_{ijk}$ denote the infection status (1=infected, 0=healthy) of child $i$ in bubble $j$ in school $k$.

If the current prevalence of COVID-19 in the population is $p$, we can estimate the number of schools/bubbles we expect to contain at least one infected child. Assuming an independent identically distributed (i.i.d.) Bernoulli distribution for infection in each individual, then the probability a group of $n$ individuals contains at least one infected individual is

$1 − (1 − p)^n$.

We can use this as a baseline estimate, but note that it is likely to be an overestimate as infections tend to cluster within groups (i.e. are not independent), and so the true probability is likely to be less than this.

The latest ONS infection survey estimates that 0.06% of the population is infected⁷. So for a bubble with n=15 children, the probability at least one of them is infected (under the i.i.d. Bernoulli model of infection) will be 0.009. If we collect data on $N=100$ primary schools, each containing 6 bubbles (three attending classes split into two bubbles each), we expect to observe 5.4 bubbles containing at least one infection in total (which is the same as the number of infected children we’d expect to see under the i.i.d. Bernoulli model). Similarly, if each school has n=90 people attending, then we’d expect there to be an infection in 5.3 schools.

How many infections would we expect to see in each bubble given it contains at least one infected child? If there is no within-school transmission, then it is likely that each infected bubble would contain only a single infected child. In this case, the effective sample size (ESS) of our data is simply the total number of children tested (100x6x15=9000). At the other extreme, imagine a disease that resulted in infection for every susceptible person who contacts an infected person. In this case, assuming infection can’t spread between school bubbles, we still expect to see 5.4 bubbles containing an infection, with 15 infected children in each bubble (or fewer if not all are susceptible), i.e., individuals within a bubble are all perfectly correlated with each other (all infected, or all healthy). In this case, only bubbles give information rather than individual children and so our effective sample size for estimating disease prevalence p is simply the number of bubbles (100 x 6 = 600). If infection spreads to everyone within a school, our sample size is effectively just the number of schools (100).

In practice, the degree of intra-bubble correlation (the Intra-Class Correlation (ICC) for bubbles) will be much less than one, but will be more than under the independent Bernoulli model (where the ICC is zero).

Hopefully, infections in children attending school will be spotted quickly (particularly in studies which test children weekly as in sKIDs), and the entire bubble will be isolated upon detection of a single infection. The effect of this will be to reduce the intra-class correlation, thus making the distribution of the number of cases per infected bubble look more like the case where there is no within-school transmission (ICC=0). This makes it more difficult to detect within-bubble or within-school transmission.

Statistical model

To compute the sample sizes needed to detect various different relative risk levels for programmes such as sKIDs, it is necessary to consider how the data will be analysed. The standard approach would be to use a multilevel mixed effects logistic regression model. As a starting point, suppose we test children both attending and not attending school. Let $x^a_{ijk}$ be covariate information about whether the child is attending school or not ($x^a = 1$ if attending, $0$ otherwise). A simple model we might consider would be

$y_{ijk} \sim \text{Bernoulli}(\mu_{ijk})$

$g(\mu_{ijk}) = \alpha + x^a_{ijk} \beta + a_k + b_k x^a_{ijk} + c_{jk} x^a_{ijk}.$

Here, $\alpha$ denotes the background risk of becoming infected. If we use the logit function $g(\mu) = \log\frac{\mu}{1 - \mu}\ $as the link function, then a prevalence of 0.06% corresponds to $\alpha =  − 7.42$. The parameter $\beta$ represents the additional prevalence within schools, and for the logit link function is equal to the log relative odds of infection in school and not in school. As an example, suppose prevalence within schools is double the general population (0.12% instead of 0.06%), i.e., the relative risk is 2, then $\beta = 0.69$. Note that after fitting this model, it is important to report not just the relative odds ($\beta$), but also the change in absolute risk ($g^{-1}(\alpha + \beta)$ vs $g^{-1}(\alpha)$).

The variables $a_k$, $b_k$ and $c_{jk}$ are the random effects, which induce correlation in infections. The model assumes that infections cluster in a school catchment area regardless of whether a child is attending school or not ($a_k$), within the children attending school ($b_k$), and within bubbles of attending children ($c_{jk}$). Typically, we’d assume Gaussian distributions for the random effects:

$a_k \sim N(0, \sigma^2_a)$,

$b_k \sim N(0, \sigma^2_b)$,

$c_{jk} \sim N(0, \sigma^2_c)$.

The variance parameters $\sigma^2_a$, $\sigma^2_b$, $\sigma^2_c$ control the degree of within-catchment, within-school, and within-bubble correlation, and can be estimated from data. In our hypothetical examples, the case where no transmission occurs in school (ICC=0) occurs when $\sigma^2_b = \sigma^2_c = 0$. A completely infectious disease for which bubbles offer good protection for children in other bubbles (i.e., infection spreads within bubble only), will have a large value for $\sigma^2_c$, and smaller value for $\sigma^2_b$. In the case of a completely infectious disease where the bubbles don’t stop between-bubble transmission, $\sigma^2_b$ would increase. COVID-19 is likely to be between these extremes. Note that a heavy-tailed distribution (rather than Gaussian) may be required for the random effects depending upon the degree of clustering observed.

In practice, we do not observe the infection status $y_{ijk}$ of a child, but instead we observe the outcome of an imperfect test. Let $d_{ijk}$ denote the test result for child $i$ in bubble $j$ in school $k$ (1=test positive, 0=test negative). The link between $d$ and $y$ reflects the accuracy of the tests:

$\text{Pr}(d=1|y=1) = 1-\text{FNR}$

$\text{Pr}(d=0|y=1) = \text{FNR}$

$\text{Pr}(d=1|y=0) = \text{FPR}$

$\text{Pr}(d=0|y=0) = 1- \text{FPR}$

where FNR is the false negative rate. The FNR depends both on the probability of a badly taken swab, and on the intrinsic sensitivity of the RT-NAAT test itself (which in turn is highly dependent on the time elapsed since initial infection). The intrinsic FNR of rate of the RT-NAAT test itself, using nasal swabs and upper throat swabs respectively, has been estimated⁸ at approximately 20% and 35% (respectively) at seven days since illness onset; thereafter it increases. When swabs are not taken by healthcare workers, or are taken from children, there is good reason to believe that badly-taken swabs may be more common, so overall FNR may well be significantly higher, possibly 40%. An overall FNR of 40% (95% CI: 25% to 55%) was assumed to be the reasonable worst-case scenario (for swabbing not performed by trained healthcare workers), in the ONS Infection Survey pilot⁹. It would be reasonable to double the sample-size to hedge against this scenario.

Sample sizes

How much data do we need to estimate $\beta$? First note that sKIDs does not plan to test children who are not attending school. Thus it can only estimate the school prevalence $\alpha + \beta$, not the increase in risk specifically from attending school, $\beta$. We could aim to detect a prevalence that is statistically different to the ONS estimate of 0.06%, i.e., test $H_0: \alpha + \beta = \text{logit}(0.0006)$ versus the one-sided¹⁰ alternative $H_1: \alpha + \beta > \text{logit}(0.0006)$. If we suppose that the prevalence in school is double the population prevalence ($\beta = 0.69$), then we can then calculate the number of children we would need to test in order to reject the null hypothesis.

We will first do the calculation assuming independent infections¹¹, and then correct this using a design effect^12,13, which is a rule-of-thumb adjustment used to allow for clustering in the design structure. A widely used design effect is $1 + (m − 1)\text{ICC}$ where $m$ is the size of a cluster and $\text{ICC}$ is the intra-class correlation. A review¹⁴ [Gul] of binary data in observational studies has shown that the $\text{ICC}$ is often of a similar order of magnitude as the prevalence (currently estimated to be 0.06%). If we assume a cluster of size 200 (a typical primary school intake), with an $\text{ICC}$ of 0.001, then the design effect suggests we need to inflate the sample size by about 20%. Using the program Sample size from the book by Machin et al¹⁵., for unclustered independent observations ($\text{ICC} = 0$), for a one-sided test with significance level 5% to have 80% power to detect a doubling of the prevalence against a known prevalence of 0.0006, we would require 13,400 observations. Inflating this for the design effect gives a sample size of 16,100. One way to account for false negative test results is to consider the FNR as we might treat dropout in a clinical trial. For example, for a dropout rate of 30%, you would typically inflate the sample size by 1/0.7=1.43, i.e. by 43%, suggesting that about 23,000 samples might be needed. This may still be an underestimate: the ONS Infection survey pilot¹⁶ considered a FNR of 40% as a reasonable worst-case point estimate, but this was for adults; for children the situation may be worse.

If the prevalence in school is only 1.5 times that of the general population (0.09% say), then to detect this increase with 80% power in unclustered data we would need to test 48,000 children, which after correcting for clustering and a 30% FNR, suggests a minimum of 82,000 tests would be needed.

The sKIDs survey intends to test children within the same class in each of four consecutive weeks, presumably because of the cost and difficulty in recruiting participating schools and children, and of setting up testing facilities within each school. Whilst four tests on any given child are not four independent samples, if an individual tests positive they are removed from the at risk set for subsequent surveys, so one individual will not contribute two positive results. Given that the infectious period for COVID-19 is approximately a week in duration, the information contained in four consecutive weekly tests on 10,000 children may be approximately equivalent to a single test of 40,000 independent children, and will additionally allow us to observe whether a detected infection spreads to other bubbles within the school.

However, the sKIDs design (testing only children attending school), is unlikely to be able to conclusively establish that the prevalence of COVID-19 in children attending school is greater than the prevalence in children not attending school as our estimate of the prevalence of COVID-19 in England is not certain (so we do not know $\alpha$ with certainty). The ONS 95% confidence interval for the prevalence is 0.02% to 0.13%, and so detecting a prevalence different to 0.06% in schools would not enable us to estimate an increased risk. Moreover, the prevalence is known to vary by as much as a factor of 10 between different regions of the UK, and within clusters at a regional level.

Our view is that a study that tests approximately 10,000 school children attending school, but doesn’t test children not attending school, is unlikely to be able to conclusively demonstrate an increased risk.

Testing non-attending children

A better approach would be to test both children attending school and children not attending school, and simultaneously estimate the prevalence in both groups (estimate αand β in the model above). Given the expectation that infections occur in clusters within communities and regions, the best way to do this would be to test children from the same school but who are not currently able to attend. For example, if children from Y6 attending school k are tested, then we should also test children from a year group not currently attending school k, such as Y5. Pairing year groups that are close in age (Y5/6 and Y1/2) will ensure that the risk of community transmission is as similar as possible for these two groups (i.e. the behaviour of Y5 children not at school will be similar to what the Y6 children would be doing were they not attending school). In addition, we should also test children who are in a year group that is permitted to attend school but are in fact not attending, allowing us to account for the fact that some parents will decide not to send their children back to school and therefore address the question around the impact of a policy decision that allows schools to re-open but does not enforce attendance. Care is needed in the analysis, and in school policy, to account for families with siblings that are in different bubbles (for example, in attending and non-attending classes). This information should be collected during testing.

Considering again the model above where we now wish to estimate α and β, a similar sample size calculation suggests that to detect a doubling of the prevalence (from 0.06% to 0.12%) in a test with 5% significance and 80% power, requires approximately 61,000 samples (split equally between the two treatment groups) if infections occur independently . Correcting for clustering and 30% false negatives, inflates this figure to approximately 105,000 tests. As before, if we test the same children in each of four consecutive weeks, this suggests approximately 26,000 children should be included in the surveillance programme (13,000 attending school, 13,000 not attending school).

Sero-surveillance

As well as RT-NAAT testing to detect the presence of SARS-CoV-2 virus in children, sKIDs also plans sero-surveillance (detecting antibodies), to estimate the proportion of children who have been exposed to COVID-19. The Weekly Coronavirus Disease 2019 Surveillance Report from PHE published on 18th June reported that a 5.5% seroprevalence was observed in May in children and adolescents (aged under 20 years). Detecting differences in prevalence rates (between attending and non-attending children) may not necessarily be any easier than with the swab tests. Firstly, without also testing children not attending school, there is no base rate to compare to, and (as before) without a reliable estimate of prevalence for the population of children, there is little value in the estimate just for children attending school. Secondly, disentangling the effect of attending school from antibody prevalence is more complicated than using active infection, as it is a result of a 6 month period history, rather than just a snapshot of the present state. Accounting for differences between regions and schools becomes more important, and so testing closely matched children attending and not attending (i.e. children from the same school) will be important in order to avoid the effect of hidden confounders. As schools open more widely, and children switch between attending and not attending school, there will be little value in comparing anit-body prevalence of these two groups.

The effect size we are looking for may well still be small. Suppose 5.5% of all children have antibodies. Considering children who have attended school since the beginning of June, if we assume they accumulate infection at a rate that is 0.1% per week higher than children not attending school, then we might expect approximately a 1% difference in the antibody prevalence between the two groups. A sample size calculation suggests we would need to test approximately 14,000 children to detect this difference in a design with independent observations. For clustered observations, adjusting using the same simple design effect as before suggests more than 25,000 subjects may need to be tested.

Detecting within-school transmission

Consider groups of children (year groups, classes, bubbles etc.) both attending and not attending school (‘bubbles’ of children not attending are hypothetical, but give a useful unit for comparison). If infections cluster within a group, particularly for those attending school, with no clustering between groups, then we expect the first infections to appear in each group at approximately the same rate. What might differ is the rate that infection spreads within a group. For those attending school, if infection in school is a problem, we expect to see multiple infections within each group. For those not in school, transmission within-group may still occur (e.g., if children socialise outside of school with children from their group), but possibly at a lower rate compared to if they were in school.

The simplest way to detect this would be to look at the distribution of case numbers per group in groups which have recorded at least a single infection. In the extreme case where there is no within-group transmission for those not attending, we’d expect cases per group to be low¹⁷. For groups attending school which contain at least one infected individual, it is hard to predict in advance how many infections we expect to observe. The distribution of case numbers will be less for groups that are part of sKIDs as the weekly testing means that infections will be detected early and the group then isolated, limiting the opportunity to learn about transmission rates.

In order to estimate within-group infection rates, we could use a generative model, such as a Reed-Frost type model (a discrete version of the continuous SIR which can simulate infections in small groups). However, the number of infected groups likely to be found by sKIDs makes it unlikely that the data will contain sufficient information to allow us to estimate infection rates with any confidence. To learn about infection within-groups, it may be better to use a targeted responsive data collection design: anytime an infection is discovered within a group attending school, the entire group could then be tested to ascertain the spread to the rest of the group. A similar approach could be used to estimate the secondary attack rate for within household transmission from children to adults.

Group testing

When the majority of primary and secondary school children return to school (most likely in September), it will be desirable to efficiently monitor COVID-19 prevalence among school children in each region of England (and indeed the UK as a whole), and also to efficiently identify and isolate COVID-19 cases among school children. (This, in turn, will be important both for suppressing transmission, and, e.g., for giving parents and teachers confidence that schools are sufficiently safe to remain open.) However, such surveillance and case-identification must be performed subject to the constraints on the available supply of RT-NAAT tests. Testing individually every school-aged child in England each week would require approximately 1.2 million NAAT tests per day, well beyond the UK’s current total NAAT-testing capacity (of approximately 200,000 NAAT tests per day). Group testing (a.k.a. ‘Batch testing’) provides a means of surveillance and case-identification, which is a great deal more efficient (both for granular surveillance, and for case-identification) than individual testing, when prevalence is low.

The idea of group testing is to pool samples together and test the ‘pooled’ samples using just one NAAT-test for each pool. If the ‘pool’ tests negative, it is likely (under modest sensitivity assumptions) that all the corresponding individuals are COVID-negative, removing the need to test individual samples. If the ‘pool’ tests positive, the positive individual can almost always be identified by pooling the samples in a different way; this can be done in parallel, so that the turnaround time is exactly the same as for individual testing. The ONS Infection Survey pilot estimates that 0.06% of the population in England is infected with COVID-19; if prevalence remains this low, or does not rise much above 1%, group testing will yield large efficiency gains.

There are various simple algorithms for group-testing, with the relative performance of different algorithms depending on the prevalence. A simple group-testing algorithm was recently trialled successfully in Rambam Hospital, Israel, and is now being rolled out commercially in Israel¹⁸; a different group-testing algorithm (Dorfman’s algorithm) was recently used in China¹⁹ to test almost 10 million people over a one-month period. The Israeli algorithm is a one-stage parallel algorithm, so it has the same turnaround time as individual testing; Dorfman’s algorithm (used in China), is a two-stage algorithm so it has twice the turnaround time of individual testing. A preprint on two-stage group-testing algorithms such as Dorfman’s algorithm, with a view to their application in RT-NAAT testing²⁰, though we remark that it does not cover the Israeli algorithm (which seems to us more promising). Another preprint, concerning more complicated group testing algorithms that have already been implemented successfully in Rwanda²¹. Roughly speaking, the basic version of the Israeli algorithm works as follows. (It works very well when the population prevalence is between approximately 0.3% and 0.7%; when prevalence is lower, other algorithms are even more efficient.) Samples are first divided into ‘big groups’ of 100. For each ‘big group’, the samples are laid out in a ten-by-ten grid. We deal with each ‘big group’ separately. Each sample in the grid is split into two halves, which are labelled ‘A-halves’ and ‘B-halves’. For each row of the grid, the ten corresponding A-halves are pooled together and tested as one pool. For each column of the grid, the ten corresponding B-halves are also pooled together and tested as one pool, at the same time as the A-halves are being tested. Provided the population prevalence is not too far above 0.5%, with high probability there will be at most one COVID-positive column and at most one COVID-positive row; from this, one can either say that there are no COVID-positive individuals in the group of 100, or else that there is exactly one (who can be identified immediately). The number of tests required is only 20, as opposed to 100; an efficiency saving of 80%. (If it is only required to identify groups, or ‘bubbles’ of 10 children with at least one COVID-19 positive individual, rather than to identify which individual is COVID-positive, then the tests on the columns can be omitted, yielding an efficiency gain of 90%. The grid-size can be increased from ten by ten to fifteen by fifteen, yielding a greater efficiency saving with ‘bubbles’ of size fifteen, which may be more standard in the schools setting.) When prevalence is significantly lower than 0.5%, variants of this algorithm with even greater efficiency savings can be used; if prevalence in the population remains at approximately 0.06% or below, then a variant of the above algorithm could yield an efficiency saving of up to 95% (and indeed, this is currently advertised commercially in Israel²²). This could bring the weekly testing of all schoolchildren in England every week within the bounds of the UK’s testing capacity, requiring on average around 60,000 tests per week - provided, as always, population prevalence does not increase too far above the current prevalence level.

We highlight that, for group testing to work well, testing of samples from school children would need to take place at county-wide centres or similar (to ensure that a localised outbreak, for example at a single school or in a single district containing a school, does not overwhelm local testing capacity), but testing at county-wide centres would certainly be feasible, given that tests are likely to be carried out weekly (or not more often than weekly); it would require van transport or similar, once per week, from each school to the county-wide testing centre. We also note that the Israeli testing scheme outlined above has used robotic arms to distribute samples; but the technology required is widely available and would be easy to implement in the UK, particularly in county-wide centres. While group-testing is slightly less sensitive than individual testing, due to the slight reduction in RT-NAAT test sensitivity after pooling, we believe the large efficiency gains (at low rates of prevalence) are highly likely to outweigh the costs, especially if the pool-size is limited to at most 16 samples per pool, as is the case with all the algorithms we have considered; see for example Yelin et al.²³. In any case, we strongly recommend that a full cost-benefit analysis of group testing for school-aged children, is performed as soon as possible, with a view to its possible implementation in September.

Causal inference

It is likely to be useful to use causal inference methods to address the following questions:

1. What is the relative risk of contracting COVID-19 for both children and staff from attending vs not attending school?

2. What is the relative risk of contracting COVID-19 for both children and staff of a policy decision to allow schools to re-open?

Not all schools have opened, and the extent to which they have reopened varies. Some primary schools have only allowed year 6 children to return, whilst others allow all children to attend at least part of the week. In addition, some parents of children who are permitted to go back to school have decided to send them to school, whereas others have not. School leadership teams decide whether to open their school - and who/how many to open to - on the basis of their school’s particular circumstances. Similarly, parents make their decision based upon their attitude to risk, but also based upon individual circumstances and risk characteristics. Factors that influence these decisions are potential confounders, in the sense that they may causally affect both the infection rate (μ) and school attendance. Some of this covariate information will be observable: denote this information as X. However, there may be confounding factors that are unobservable, which we’ll denote by U. A causal network showing the structure of the problem is shown below.

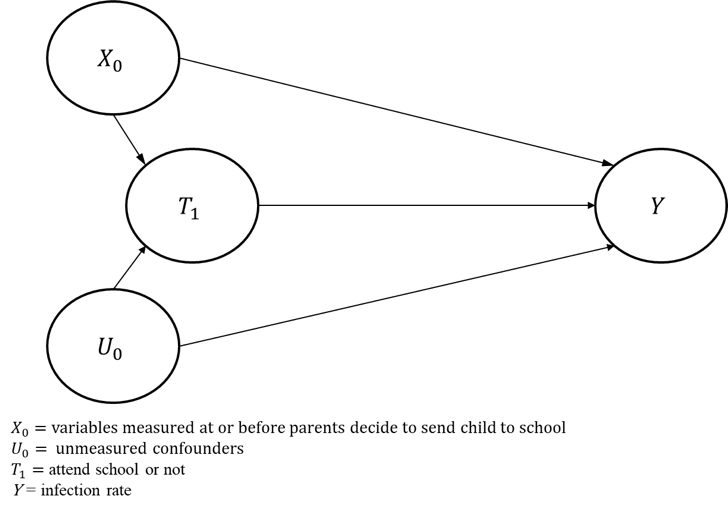
Additional covariate information could, in theory, be used to control for confounding factors in a model to estimate the effect of attending school on the infection rate - thereby blocking the T←X→Y path in the above diagram - though unmeasured confounders could still bias the estimate of the effect of attending school on the infection rate. In addition, it is possible that factors that vary over time (such as the local infection rate) could influence the school attendance decision and the infection rate - thus time-dependent confounding could be present. In that case, more sophisticated analytical techniques would be required, such as inverse probability weighting.

Individual level covariates that it would be useful to collect include

• Is the individual a student or teacher (or other staff member)? This would allow us to calculate the risk to teachers from being in school.

• Is the individual currently attending school?

• Do children live with a sibling (or other child) currently attending school, and are they in the same school and same bubble within the school? For example, it may be prudent to remove Y5s who have a Y6 sibling attending school from the analysis, to avoid complicating the analysis with household transmission resulting from school opening.

• For parents of children not attending school, ask ‘Would you have sent your child to school if you could have done so?’ Infection risk is confounded by parents’ decision to send their children to school. Acquiring this information would potentially allow unmeasured confounders which affect parent choice to be accounted for in the analysis.

School level information that should be collected includes

• What bubble size (if any) is being implemented within the school?

• How many children/bubbles are in attendance?

• Demographic information

• Physical space available to the school

It is also important to note that the policy approach taken to re-opening schools introduces the possibility of undertaking causal analyses that are less prone to confounding bias, through the use of instrumental variables. An instrument must induce change in the explanatory variable (attending school, or being allowed to go to school, depending upon the specific question being addressed) but must have no independent effect on the dependent variable (infection rate). A child’s year group fulfils this requirement, because in most schools only specific year groups have been permitted to return to school, and because year group is unlikely to be an independent cause of infection.

In a randomised controlled trial (RCT), randomisation is the instrument that allows the effectiveness of being assigned to different groups to be compared. In the case of re-opening schools for specific year groups, year group represents our proxy for randomisation. Note that this most accurately holds true for the second of our research questions, that of “What is the relative risk of contracting COVID-19 for both children and staff of a policy decision to allow schools to re-open?”. For this question, using Y5 and Y6 children to illustrate the point and assuming that the same set of schools are used for both attenders and non-attenders, we would compare all Y6 children (whether or not they actually go back to school) to all Y5 children (who are not allowed to go back to school). Here the instrument would appear to be ideal, because the causal effect being estimated is that associated with the policy decision. The policy decision allows schools to re-open, but some may choose not to, and some parents may choose not to allow their children to return to school - but this is fine, because we are just interested in estimating the effect of the policy decision. For this analysis, confounding could remain if children who do not return to school have siblings who do return to school, and therefore it is important to collect information on siblings to allow this to be addressed.

For the first of our research questions, that of “What is the relative risk of contracting COVID-19 for both children and staff from attending vs not attending school?”, the year group instrument is still valid, because attendance at school will be associated with year group. However, the instrument no longer seems ideal, because here we are attempting to estimate the causal effect of attendance at school, but attendance at school is not only determined by year group - it is also influenced by patient (and school) choice. Therefore, for this causal effect, confounding factors may remain. It may be possible to control for these using the variables outlined above.

Whilst we believe that current circumstances present an ideal opportunity to collect data that will allow us to conduct the analyses described above, it is prudent to note that the low infection rate means that the analyses are likely to provide results that are subject to substantial uncertainty. Nevertheless, valuable information could be obtained.

Conclusions and recommendations for the design of causal infection testing

• We still have limited understanding about COVID-19 disease in children. Thus, comparing the infection rate in children in a school with the infection rate in the general population is fraught with difficulty. In addition, school facilities, contact between children outside of school, and regional infection rates all vary significantly, and so the background risk for children may differ substantially from school to school (whether attending or not). Thus it is important to collect matched samples of children both attending and not attending school. The simplest way to do this is to test year groups both attending and not attending the same school, e.g., test Y1 and Y6 (attending) as well as Y2 and Y5 (typically not attending) from the same school. It is important also to collect data from children at these schools who are permitted to return to school, but who have not returned.

• Detecting a doubling of the prevalence in school will require approximately 95,000 tests given the current estimate of disease prevalence. Testing 12,000 children attending school, and 12000 children not attending, for four consecutive weeks may be sufficient.

• Testing children not in school may be logistically more difficult than testing those in school. However, even a single test (i.e. not the four weekly tests planned for attending children in sKIDs) of (matched) children not currently attending school would provide useful information that would better allow us to detect an increase in prevalence.

• Collect covariate information on schools and pupils. In particular, ask the parents of children who are tested but who are not attending school the question “Would you have sent your child to school if you could?” School attendance is optional at present, and the level of risk taken by individual families will vary (e.g. households may contain shielding individuals). This is a confounder between the decision to send children to school and their risk of infection. Collecting this information from non-attending children may allow this to be accounted for. Collecting information on siblings, and whether they are attending school, is also important.

• To estimate transmission rates within a school, responsive testing that focuses on school with a confirmed infection may be necessary. Children within bubbles in which an infection is discovered will have to self-isolate for 7/14 days. Given that swab tests can be unreliable in the early stages of infection, testing should continue for these children during their isolation period.

• The sample of schools should be carefully stratified to reflect the range of UK school types, and the variation in Infection rates between regions.

Footnotes and References

1. Munro A. and Goldstein H. (2020) An evidence summary of Paediatric COVID-19 literature. Don’t Forget the Bubbles. 2020 Apr. doi: 10.31440/DFTB.24063. ↩

2. Zhang, J. et al. (2020) Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science. doi: 10.1126/science.abb8001 ↩

3. Some confounding will remain due to parental choice in the decision about whether to send children who are eligible to attend to school or not. See below for more detail. ↩

4. With the possibility of a further opportunity in September depending upon how school openings are staggered. ↩

5. Ladhani, S. et al (2020) COVID-19 Surveillance in Children attending preschool, primary and secondary schools. Available at: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/891762/sKID_protocol_v1.3.pdf ↩

6. Many schools currently operate a ‘protective bubble’ system, which are typically groups of no more than 15 children. Contact between children within a bubble is tolerated, but contact between bubbles is discouraged. The ability to implement a bubble system varies between schools, and will change as the government relaxes social distancing rules. ↩

7. This is a prevalence estimate for the entire population, not just children. ↩

8. Wikramaratna, P., Paton, R., Ghafari, M., Lourenco, J. (2020) Estimating false-negative detection rate of SARS-CoV-2 by RT-PCR, medRxiv 2020.04.05.20053355;doi: 10.1101/2020.04.05.20053355. ↩

9. Office for National Statistics (2020) Coronavirus (COVID-19) Infection Survey Pilot. England, 12 June 2020. Available at: https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/conditionsanddiseases/bulletins/coronavirusCOVID19infectionsurveypilot/12june2020 ↩

10. We are less interested in the case where prevalence in school is lower than the general population. ↩

11. If infections occur independently (i.e., they don’t cluster within bubbles) then the effective sample size of the design is simply the total number of people tested. ↩

12. Rowe A. K., Lama, M., Onikpo, F., and Deming, M. (2002). Design effects and intraclass correlation coefficients from a health facility cluster survey in Benin. International Journal for Quality in Health Care. 14 (6): 521–523. doi: 10.1093/intqhc/14.6.521 ↩

13. Kish, L. (1965). “Survey Sampling”. New York: John Wiley & Sons, Inc. ISBN 0-471-10949-5. ↩

14. Gulliford, MC., Adams, G., Ukoumunne, OC., Latinovic, R., Chinn, S., Campbell, MJ. (2005) Intraclass correlation coefficient and outcome prevalence are associated in clustered binary data. Journal of clinical epidemiology. 2005 Mar 1;58(3):246-51. doi: 10.1016/j.jclinepi.2004.08.012 ↩

15. Machin, D., Campbell, MJ., Tan, SB., Tan, SH. (2018) Sample sizes for clinical, laboratory and epidemiology studies. John Wiley & Sons; 2018 Aug 20. ↩

16. Office for National Statistics (2020) Coronavirus (COVID-19) Infection Survey Pilot. England, 12 June 2020. Available at: https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/conditionsanddiseases/bulletins/coronavirusCOVID19infectionsurveypilot/12june2020 ↩

17. For a group of size 30 with infections occurring independently with probability 0.06% (i.e., no within-group transmission), conditional upon the group containing a single infected individual, there is a less than 1% chance that the group contains more than a single infected individual. ↩

18. See https://www.lesstests.com/ ↩

19. BBC News (2020) Coronavirus: China’s plan to test everyone in Wuhan, 8 June 2020, Available at: https://www.bbc.co.uk/news/world-asia-china-52651651 ↩

20. Aldridge, M. (2020) Conservative two-stage group testing. Available at: https://arxiv.org/abs/2005.06617 ↩

21. Mutesa, L. et al (2020) A strategy for finding people infected with SARS-CoV-2: optimizing pooled testing at low prevalence. Available at: https://arxiv.org/abs/2004.14934 ↩

22. See https://www.lesstests.com/ ↩

23. Yelin, I et al (2020) Evaluation of COVID-19 RT-qPCR Test in Multi sample Pools. In Clinical Infectious Diseases, ciaa531, doi: 10.1093/cid/ciaa531 ↩